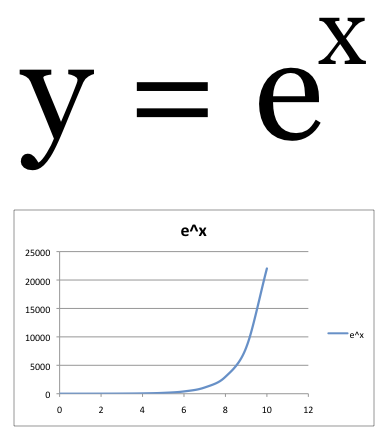
With increasing frequency, I'm finding myself in a conversation with a seemingly smart person in which there seems to be a fundamental misunderstanding about the properties of an exponential function. And the lack of a fundamental understanding of the exponential have grave consequences -- we may draw incorrect conclusions that have huge errors because of it. Albert A. Bartlett perhaps said it best,
"The greatest shortcoming of the human race is our inability to understand the exponential function."
Mark Zuckerberg, maybe paraphrasing Barlett recently said, "" I'll give Zuckerberg the benefit of the doubt -- he made a mistake and really does have a pretty good grasp of the exponential function.
And, perhaps creating the greatest confusion of all is Ray Kurzweil, a thinker and engineer I respect immensely. Kurzweil is predicting that the Singularity is Near because we are at the "knee of the curve" of some important trends that are changing exponentially -- a "point" in time where things start to change a lot faster. However, there is an important fallacy here:
There is no such thing as a knee to an exponential function.
I say this with all due respect to Mr. Kurzweil, who is is clearly much smarter than me.
Why We Are Fooled
When we look at the graph of an exponential function, our visual sensors (ahem, our eyes) seem to fool us. Isn't it "obvious" where the knee of the curve is? In fact, it's not obvious that there isn't a knee. The knee always seem to be at the right "edge" of the displayed graph. In the illustration below, the knee appears to be at a different place depending on the position where we examine x.
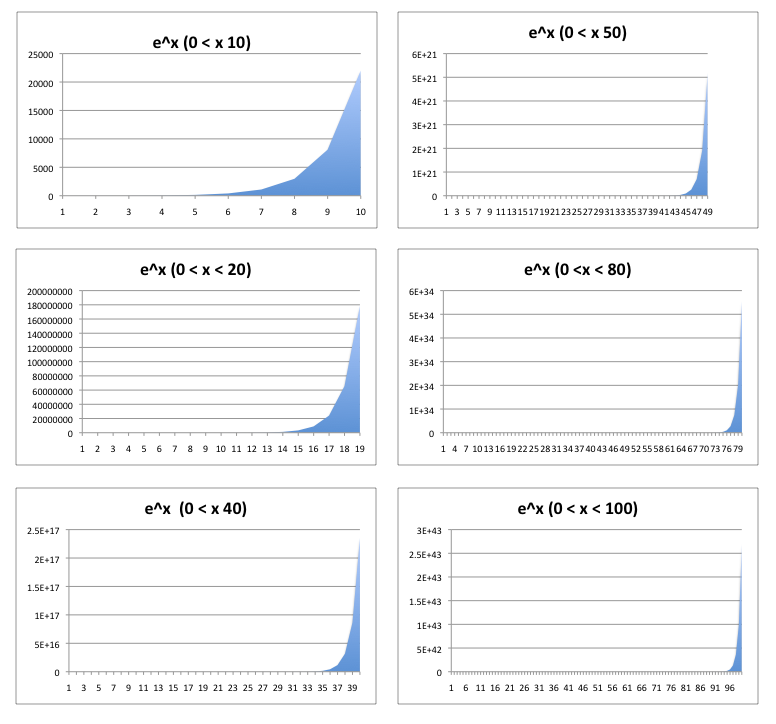
How can this be?
It's not completely clear to me why we are fooled. But basically, I think it has something to do with the idea that regardless of where your observation point is, looking "left" always looks flat and small, while looking "right" always looks steep. For example, consider where we are at with hard disk drive densities. Today, we see that 1 terabyte hard disks are common place at less than $100. But, 10 years ago, $100 bought you roughly a 1 gigabyte hard disk. That feels pretty small but understandable. Looking back, the curve looks pretty flat, appearing to change only very slowly. In fact, though, it's growing exponentially. Looking forward 10 years, we'll have a 1 petabyte drive for $100. And the pace looks amazingly fast. And it's pretty hard to imagine what a "normal" consumer would do with a petabyte.
Still not convinced that there is no knee to the exponential curve? Well, consider when we plot an exponential at log scale. There is no loss of information when we do this. Seems like we should be able see that knee in the curve. But of course, it's line. At log scale, the visual representation of the plot log(e^x) = x.
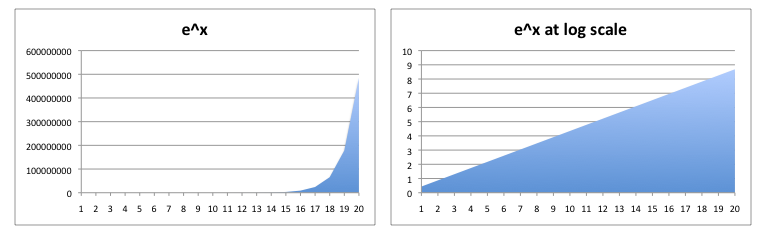
At linear scale, it looks like the "knee of the curve" is somewhere around at 18. However, when we look at it at log scale, our eyes tell us nothing.
Why Does This Matter?
"So what?," you might be asking yourselves. Is this all academic wankerage? Does it matter in any practical terms? Indeed, I think it does. Our failures to understand how fast the exponential function grows might lead us to bad economic decisions. Albert Einstein is attributed with saying that, "The most powerful force in the universe is compound interest" -- a hat tip to the our lack of understanding of the exponential function. And, anyone that has heard the argument why you should start putting money into a 401(k) plan earlier rather than later has probably been told some dubious story about the power of compound interest/exponential growth. And, because the math behind the theory of our economy is based on formulas including exponentials, it's frightening that most politicians don't grok the exponential either. Chris Martenson tells a good story regarding the perilous situation we are in. Agree with him or not, it's good food for thought. Not understanding the power of the exponential will result in us making bad decisions. Finally, the next time you hear some some talk about exponential growth with just a data point or two (or three), be very weary -- such "curve fitting" is an error due to mathematical ignorance at best or deliberately misleading as worst.
Second, as software engineers, we should be careful not to implement solutions that run in exponential time. And, in considering the problems we are attempting to solve, we should understand why it might be theoretically impossible to find a solution that we can't solve in less than exponential time and therefore seek to define different problems to solve. Or implement a heuristic instead. Such analysis allows us to understand the "boundary of the solution space" for the problems we want to solve. While this might all sound like theoretical esoteria, understanding these algorithm complexities makes us better engineers. In short, understanding the potentially intractability of solving some problems in less than reasonable/"exponential" time is perhaps the most important unanswered question in theoretical computer science. (Note: For the non-computer scientists, I apologize for the vague and jargon rich language here in this paragraph.)
Last, for entrepreneurs, I'm sure you've run into venture capitalists that are all hot on businesses that are growing purportedly virally/exponentially. And, of course, in attempts to make a good investment, they want to put money in at the "knee of the of curve" (or where the curve "hockey sticks"). "Where is it?" you are asked. You should think carefully about how you are going to answer this question that doesn't quite make sense. It's quite the "gotcha."
Hopefully, you have an understanding of the math of the exponential function and why we are often seduced by it. Then you won't be fooled by faulty thinking, and, further, you can build a rhetorical argument around the magic of the exponential function for your own gain. Good luck!

